La probabilidad es área: una forma intuitiva de entender eventos

Cuando hablamos de probabilidad, a menudo pensamos en números entre 0 y 1, fracciones o porcentajes. Pero existe una forma geométrica e intuitiva de entender la probabilidad:
la probabilidad es área.

¿Qué significa que la probabilidad sea área?

La probabilidad de que ocurra un evento puede representarse como la proporción del área total correspondiente a ese evento dentro del espacio de todos los posibles resultados.

Imagina un espacio de resultados como un rectángulo o un círculo que representa todos los resultados posibles de un experimento.

• Cada punto dentro de este espacio es un resultado posible.
• Un evento es una región dentro de ese espacio.
• La probabilidad del evento es el área de esa región dividida entre el área total.

Ejemplo con un dado “geométrico”

Supongamos que lanzamos un dado y queremos visualizarlo en un diagrama rectangular:

• Cada resultado (1, 2, 3, 4, 5, 6) ocupa el mismo “espacio” dentro del rectángulo.
• El área de cada sección es igual, así que la probabilidad de cada resultado es:

$$P(\text{resultado}) = \frac{\text{área de la sección}}{\text{área total}} = \frac{1}{6}$$

Aquí, área = probabilidad.
Este enfoque funciona incluso si el dado está sesgado: las áreas de cada sección cambian según la probabilidad, pero la suma de todas las áreas sigue siendo 1.

Distribuciones continuas

El concepto de probabilidad como área es fundamental en variables continuas, donde los resultados posibles no son discretos. Por ejemplo, si lanzamos un dado “perfectamente continuo” que puede dar cualquier valor entre 0 y 1, entonces:

• No podemos hablar de un solo resultado: la probabilidad de un valor exacto es 0.
• Pero podemos calcular la probabilidad de un intervalo, que es proporcional al área bajo la curva de densidad.

Esto es la base de la probabilidad continua y la función de densidad (PDF):

$$P(a \leq X \leq b) = \int_{a}^{b} f(x) dx$$

Aquí, la integral representa el área bajo la curva entre los puntos a y b, y esa área es la probabilidad de que X esté en ese intervalo.

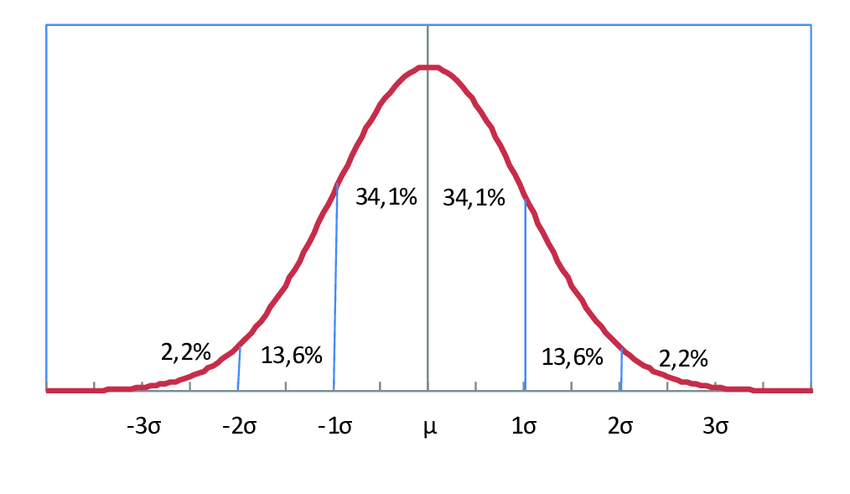
Visualizando la probabilidad como área

Una forma muy clara de entenderlo es mediante un diagrama de rectángulos o gráficos de barras:

• Cada barra representa un resultado posible.
• La altura de la barra corresponde a la “densidad” o probabilidad.
• El área de la barra es proporcional a la probabilidad del resultado.

En variables continuas, reemplazamos las barras por curvas suaves.

• Por ejemplo, la distribución normal es una curva de campana:
• La probabilidad de un intervalo es el área bajo la curva en ese intervalo.

Aplicaciones prácticas

Visualizar la probabilidad como área tiene ventajas:

1. Intuición inmediata: Nos ayuda a “ver” los eventos probables y menos probables.
2. Distribuciones continuas: Fundamental en estadística, machine learning y análisis de datos.
3. Comparación de eventos: Podemos comparar fácilmente qué evento es más probable observando qué área ocupa.
4. Simulaciones y Monte Carlo: Al generar puntos aleatorios dentro de un espacio, contar cuántos caen dentro de un evento es equivalente a calcular el área y, por lo tanto, la probabilidad.

En resumen

• La probabilidad puede visualizarse como área dentro de un espacio de resultados.
• En eventos discretos, el área es proporcional a la fracción de resultados posibles.
• En variables continuas, la probabilidad es el área bajo la curva de densidad.
• Este enfoque conecta geometría y estadística, haciendo que la probabilidad sea más intuitiva y visual.