Los conjuntos son uno de los conceptos más básicos y a la vez más importantes en estadística y probabilidad. Toda la teoría de la probabilidad —y, por extensión, gran parte del análisis estadístico— se construye sobre la teoría de conjuntos, que nos permite describir y razonar sobre eventos, muestras y resultados posibles.
¿Qué es un Conjunto?
Un conjunto es una colección bien definida de elementos, que pueden ser números, personas, objetos o resultados de un experimento.
En estadística, usamos conjuntos para describir:
- El espacio muestral (todos los resultados posibles de un experimento).
- Los eventos (subconjuntos del espacio muestral).
- Las relaciones entre distintos eventos.
Por ejemplo:
Si lanzamos un dado, el espacio muestral es
$$S = {1, 2, 3, 4, 5, 6}$$
Un evento puede ser “obtener un número par”:
$$A = {2, 4, 6}$$
Operaciones entre Conjuntos
Las operaciones entre conjuntos reflejan relaciones entre eventos en probabilidad.
| Operación | Descripción | Símbolo | Ejemplo (en el dado) |
|---|---|---|---|
| Unión | Ocurre A o B (o ambos) | \(A \cup B\) | “Número par o mayor que 4” |
| Intersección | Ocurre A y B a la vez | \(A \cap B\) | “Número par y mayor que 4” |
| Complemento | No ocurre A | \(A’\) o \(A^c\) | “Número impar” |
| Diferencia | Elementos en A que no están en B | \(A – B\) | “Números pares que no son mayores que 4” |
Estas operaciones son la base del cálculo de probabilidades, porque cada evento se asocia con un conjunto de resultados, y las reglas de probabilidad siguen las mismas leyes que los conjuntos (como las Leyes de De Morgan).
Ejemplo Práctico en Python
Podemos representar los conjuntos y operaciones anteriores fácilmente con set:
# Espacio muestral del lanzamiento de un dado
S = {1, 2, 3, 4, 5, 6}
# Eventos
A = {2, 4, 6} # número par
B = {4, 5, 6} # número mayor que 3
# Operaciones entre conjuntos
union = A | B
interseccion = A & B
complemento = S - A
diferencia = A - B
print("A ∪ B =", union)
print("A ∩ B =", interseccion)
print("A' =", complemento)
print("A - B =", diferencia)Salida:
A ∪ B = {2, 4, 5, 6}
A ∩ B = {4, 6}
A' = {1, 3, 5}
A - B = {2}Conjuntos y Probabilidad
En la teoría de la probabilidad, los conjuntos se usan para definir y combinar eventos.
La probabilidad de un evento \( A \) se define como la proporción de casos favorables respecto al total de casos posibles:
$$P(A) = \frac{|A|}{|S|}$$
Ejemplo:
$$S = {1,2,3,4,5,6}, \quad A = {2,4,6}$$
$$P(A) = \frac{3}{6} = 0.5$$
En Python, podemos calcularlo así:
S = {1,2,3,4,5,6}
A = {2,4,6}
P_A = len(A) / len(S)
print(f"P(A) = {P_A}")Salida:
P(A) = 0.5Leyes de De Morgan en Probabilidad
Las Leyes de De Morgan conectan los conceptos de unión, intersección y complemento, tanto en conjuntos como en eventos probabilísticos:
$$(A \cup B)’ = A’ \cap B’$$
$$(A \cap B)’ = A’ \cup B’$$
Estas leyes permiten simplificar cálculos y entender mejor la relación entre eventos.
Verificación en Python: assert no devuelve ningún valor. Es una instrucción de verificación:
- Si la condición es verdadera, no hace nada.
- Si la condición es falsa, lanza un AssertionError.
U = {1, 2, 3, 4, 5, 6}
A = {1, 2, 3}
B = {3, 4, 5}
# Leyes de De Morgan:
# (A ∪ B)' = A' ∩ B'
# (A ∩ B)' = A' ∪ B'
assert U - (A | B) == (U - A) & (U - B)
assert U - (A & B) == (U - A) | (U - B)
print("Ambas leyes de De Morgan se verifican correctamente.")Representación Visual: Diagramas de Venn
En estadística, los diagramas de Venn son una herramienta visual para representar eventos y sus intersecciones.
En Python podemos generarlos fácilmente:
from matplotlib import pyplot as plt
from matplotlib_venn import venn2
A = {1, 2, 3, 4, 5}
B = {4, 5, 6, 7, 8}
union = A | B
interseccion = A & B
diferencia = A - B
print("A ∪ B:", union)
print("A ∩ B:", interseccion)
print("A - B:", diferencia)
venn2([A, B], set_labels=('A', 'B'))
plt.title("Operaciones entre conjuntos")
plt.show()Union - A ∪ B: {1, 2, 3, 4, 5, 6, 7, 8}
Interseccion - A ∩ B: {4, 5}
Diferencia - A - B: {1, 2, 3}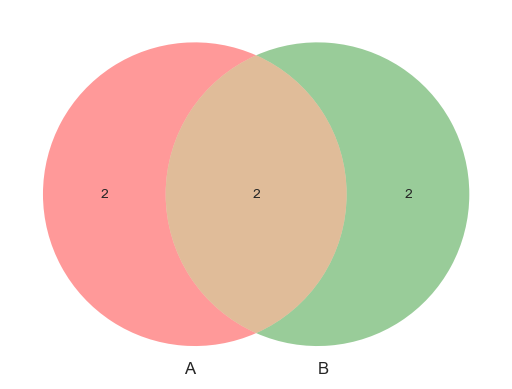
Estos gráficos son muy útiles al enseñar reglas de probabilidad, interdependencia de eventos y espacios muestrales.
En Resumen
| Concepto | En Estadística | En Python |
|---|---|---|
| Espacio muestral | Todos los resultados posibles | set() |
| Evento | Subconjunto de resultados | subconjunto de set() |
| Probabilidad | \(P(A)\) | A |
| Unión de eventos | \(A \cup B\) | `A |
| Intersección | \(A \cap B\) | A & B |
| Complemento | \(A’\) | S - A |
| Diferencia | \(A – B\) | A - B |