Ecuaciones Lineales

¿Por Qué las Ecuaciones Lineales Son Clave en Data Science?

Las ecuaciones lineales y los sistemas lineales son como el esqueleto de la data science. Son la base de algoritmos como la regresión lineal, los sistemas de recomendación y el análisis de datos en general. Imagina que cada punto de datos es una pieza de un rompecabezas: las ecuaciones lineales te ayudan a juntar las piezas para descubrir patrones.

«Sin ecuaciones lineales, no habría machine learning moderno. Son el primer paso para transformar datos en decisiones.»

¿Qué es una Ecuación Lineal?

Una ecuación lineal es una ecuación donde las variables están elevadas a la potencia 1 y multiplicadas por un coeficiente (no hay cuadrados ni raíces) y se combinan con sumas o restas.

Ejemplo Simple

$$3x + 2y = 30$$

Como concepto esta bien. ¿pero cual es el sentido de esto? ¿de donde sale? La idea base de la ecuación lineal es una relación constante entre dos cosas. La ecuación lineal nace cuando dos magnitudes cambian de forma proporcional.

Por ejemplo:

Si vendes café a 2€ cada uno, el ingreso total depende linealmente del numero de cafés vendidos.

$$Ingreso = 2 \times \text{Número de cafés}$$

Esto puede escribirse matemáticamente como

$$y = 2x$$

Donde:

x, y: Variables (Ingreso, Café.)
2: Coeficientes (pesos de las variables)

Esa es una relación lineal: cada vez que $x$ aumenta 1, $y$ aumenta 2. La tasa de cambio es constante. Visualmente esta ecuación representa una línea recta en un plano. Cada solución $(x, y)$ es un punto en esa línea.

De ahí el nombre de lineal, porque describe una relación que se representa como una línea recta en un gráfico. Las ecuaciones lineales modelan situaciones donde:

el cambio es constante,
la relación entre variables es directa o proporcional.

Por eso son la base de la modelización matemática, antes de llegar a modelos más complejos, todo empieza por asumir una relación lineal.

Representar las ecuaciones

En la forma general o modelo pendiente e intersección, toda ecuación lineal puede escribirse así:

$$y=mx+b$$

Donde:

$b$ –> es el valor inicial o intersección con el eje Y: el valor de $y$ cuando $x=0$.
$y$ –> valor en el eje vertical (dependiente)
$x$ –> valor en el eje horizontal (independiente)
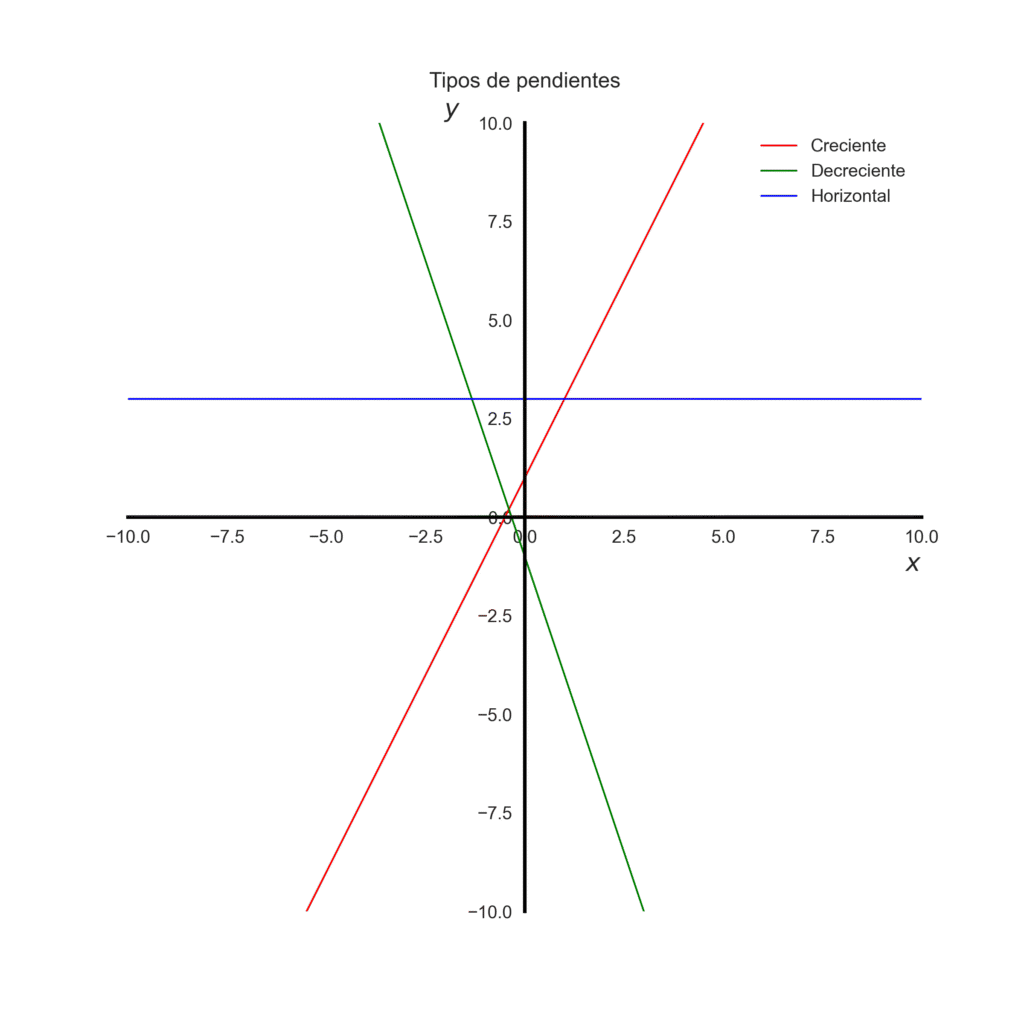
$m$ –> es la pendiente, cuánto cambia $y$ cuando $x$ aumenta una unidad.
- Si $m > 0$ –> sube hacia la derecha (creciente)
- Si $m < 0$ –> baja hacia la derecha (decreciente)
- Si $m = 0$ –> la recta es horizontal

Código de la grafica

Código Python con Matplotlib

import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(8,8))
ax.axline((0, 1), slope=2, color="red", linewidth=1, label="Creciente")
ax.axline((0, -1), slope=-3, color="green", linewidth=1, label="Decreciente")
ax.axline((0, 3), slope=0, color="blue",linewidth=1, label="Horizontal")

# Ejes en el centro
ax.spines['left'].set_position('zero')   # eje Y en x=0
ax.spines['bottom'].set_position('zero') # eje X en y=0

# Quitar bordes superior y derecho
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)

# Cambiar color y grosor de los ejes (spines)
for spine in ['left', 'bottom']:
    ax.spines[spine].set_color('black')
    ax.spines[spine].set_linewidth(2)

# Límites y cuadrícula
ax.set_xlim(-10, 10)
ax.set_ylim(-10, 10)

# tamaño de los numeros
ax.tick_params(axis='both', which='major', labelsize=10)

# Etiquetas y leyenda
ax.set_xlabel(r"$x$", fontsize=14, loc="right")
ax.set_ylabel(r"$y$", fontsize=14, loc="top", rotation=0)
ax.legend()
ax.set_title("Tipos de pendientes", pad=20)
ax.legend(facecolor='none', edgecolor='none')
ax.grid(False)
plt.savefig("pendientes.png", transparent=True, dpi=300)
plt.show()

import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(8,8))
ax.axline((0, 1), slope=2, color="red", linewidth=1, label="Creciente")
ax.axline((0, -1), slope=-3, color="green", linewidth=1, label="Decreciente")
ax.axline((0, 3), slope=0, color="blue",linewidth=1, label="Horizontal")

# Ejes en el centro
ax.spines['left'].set_position('zero')   # eje Y en x=0
ax.spines['bottom'].set_position('zero') # eje X en y=0

# Quitar bordes superior y derecho
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)

# Cambiar color y grosor de los ejes (spines)
for spine in ['left', 'bottom']:
    ax.spines[spine].set_color('black')
    ax.spines[spine].set_linewidth(2)

# Límites y cuadrícula
ax.set_xlim(-10, 10)
ax.set_ylim(-10, 10)

# tamaño de los numeros
ax.tick_params(axis='both', which='major', labelsize=10)

# Etiquetas y leyenda
ax.set_xlabel(r"$x$", fontsize=14, loc="right")
ax.set_ylabel(r"$y$", fontsize=14, loc="top", rotation=0)
ax.legend()
ax.set_title("Tipos de pendientes", pad=20)
ax.legend(facecolor='none', edgecolor='none')
ax.grid(False)
plt.savefig("pendientes.png", transparent=True, dpi=300)
plt.show()

¿Por qué las pendientes siempre avanzan a la derecha?

Esto tiene que ver con cómo definimos el sistema de coordenadas cartesianas y el concepto de pendiente. Vamos a desglosarlo paso a paso:

La pendiente mide cuánto cambia $y$ cuando $x$ cambia una unidad.
Cuando calculamos la pendiente avanzamos de izquierda a derecha en el eje $x$.
Entonces la pendiente se interpreta como el cambio vertical que ocurre al movernos a la derecha.
Por eso, al dibujar la recta, decimos que “avanza a la derecha” y sube o baja según $x$.
Si quisieras avanzar a la izquierda, sería simplemente $x<0$ y la pendiente seguiría siendo la misma, solo que la “mirada” sería desde el otro extremo.

En otras palabras: no es que la recta no exista hacia la izquierda, sino que matemáticamente la pendiente se mide tomando $Δx$ (variación de x) positivo, lo que corresponde a moverse hacia la derecha.

El sentido algebraico: equilibrio

Desde el punto de vista algebraico, una ecuación es una igualdad entre dos expresiones que mantiene un equilibrio. Una ecuación lineal representa un equilibrio simple, sin potencias ni productos entre variables:

$$2x+3y=30$$

Significa que existen valores de $x$ y $y$ para los cuales la expresión de la izquierda $2x+3y$) tiene el mismo valor que el número de la derecha (30).

Cada punto $(x,y)$ que cumple esa igualdad está en equilibrio: pertenece a la recta.
Ambos lados deben ser iguales para que la ecuación se cumpla.
Una ecuación representa una condición de equilibrio o una restricción sobre los valores posibles de las variables.

Desde el punto de vista algebraico, lo que hacemos con una ecuación es buscar los valores de las variables que la hacen verdadera. A eso lo llamamos resolver la ecuación. En este caso: $2x+3y=30$ no tiene una única solución, sino infinitas combinaciones de $(x,y)$ que cumplen la igualdad (todas las que están sobre la recta).

Si representamos todos los puntos $(x,y)$ que cumplen esa ecuación, obtenemos una recta en el plano cartesiano. Así, una ecuación lineal de dos variables es la expresión algebraica de una recta.

Ejemplo: Ecuación linear de las frutas

Un problema clásico seria resolver cuantas manzanas y naranjas podemos comprar con 30€, donde las manzanas tienen un precio de 2€ y las naranjas de 3€. (Supón que puedes fraccionar las frutas).

Este problema se resuelve con un ecuación lineal que se representa como sigue:

$$2x + 3y = 30$$

Donde:

2 y 3 –> son los coeficientes (precios de las frutas)
$x$–> variable que representa las manzanas
$y$ –> variable que representa las naranjas
30 –> es el termino independiente (la constante)

Representamos la ecuación en la forma general $y=mx+b$:

$$3y = -2x + 30$$

Pasamos el 3 dividiendo y calculamos:

$$y = \frac{2}{3}x – \frac{30}{3}$$

$$y = -\frac{2}{3}x + 10$$

Aquí tenemos:

$m = – \frac{2}{3}$ –> pendiente de la recta.
$b = 10$ –> la ordenada en el origen, o sea el punto donde la recta corta el eje Y.
Cuando $x=0$: $y=10$ –> la recta pasa por el punto $(0, 10)$.
Cuando $y=0$: $x=15$ → la recta pasa por el punto (15, 0):

$$2x + 3y = 30$$

$$2x + 3(0) = 30$$

$$2x = 30$$

$$2x = \frac{30}{2}$$

$$x = 15$$

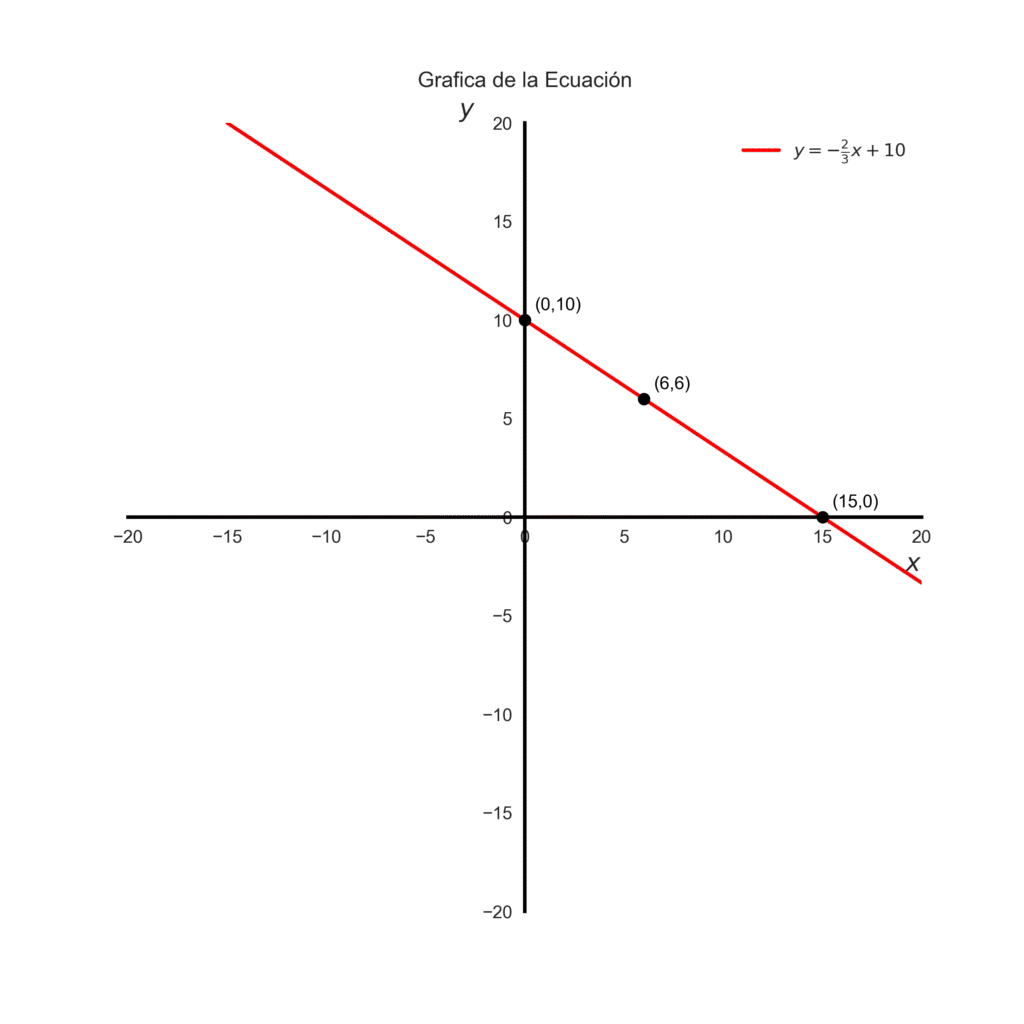
Entonces tenemos ya dos puntos $(0,10)$ y $(15,0)$. Con estos dos puntos podemos trazar una recta que representa la ecuación. Cada punto en la recta, es una combinación de manzanas($x$) y naranjas ($y$) que equivalen a una compra de 30€.

Podemos calcular mas combinaciones de frutas posibles eligiendo los valores de $x$ y calculando $y$ en la ecuación de la forma pendiente – intersección.

Por ejemplo, si $x = 6$:

$$y = – \frac{2}{3}x + 10$$

$$y = – \frac{2}{3}(6) + 10$$

$$y = – \frac{12}{3} + 10$$

$$y = – 4 + 10 = 6$$

Otra combinación de frutas y punto en la grafica seria $(6,6)$. Representemos gráficamente la ecuación.

Código de la grafica

Código Python de Matplotlib

import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(8,8))
ax.axline((0, 10), slope=-2/3, color="red", linewidth=2, label=r"$y = -\frac{2}{3}x + 10$")

# Puntos específicos
puntos = [(15,0), (0,10), (6,6)]
for x, y in puntos:
    ax.plot(x, y, 'ko', markersize=6)              # dibujar punto
    ax.text(x + 0.5, y + 0.5, f"({x},{y})", fontsize=10, color='black')

# Ejes en el centro
ax.spines['left'].set_position('zero')   # eje Y en x=0
ax.spines['bottom'].set_position('zero') # eje X en y=0

# Quitar bordes superior y derecho
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)

# Cambiar color y grosor de los ejes (spines)
for spine in ['left', 'bottom']:
    ax.spines[spine].set_color('black')
    ax.spines[spine].set_linewidth(2)

# Límites y cuadrícula
ax.set_xlim(-20, 20)
ax.set_ylim(-20, 20)

# tamaño de los numeros
ax.tick_params(axis='both', which='major', labelsize=10)

# Etiquetas y leyenda
ax.set_xlabel(r"$x$", fontsize=14, loc="right")
ax.set_ylabel(r"$y$", fontsize=14, loc="top", rotation=0)
ax.legend()
ax.set_title("Grafica de la Ecuación", pad=20)
ax.legend(facecolor='none', edgecolor='none')
ax.grid(False)
plt.savefig("ecuacion de las frutas.png", transparent=True, dpi=300)
plt.show()

import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(8,8))
ax.axline((0, 10), slope=-2/3, color="red", linewidth=2, label=r"$y = -\frac{2}{3}x + 10$")

# Puntos específicos
puntos = [(15,0), (0,10), (6,6)]
for x, y in puntos:
    ax.plot(x, y, 'ko', markersize=6)              # dibujar punto
    ax.text(x + 0.5, y + 0.5, f"({x},{y})", fontsize=10, color='black')

# Ejes en el centro
ax.spines['left'].set_position('zero')   # eje Y en x=0
ax.spines['bottom'].set_position('zero') # eje X en y=0

# Quitar bordes superior y derecho
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)

# Cambiar color y grosor de los ejes (spines)
for spine in ['left', 'bottom']:
    ax.spines[spine].set_color('black')
    ax.spines[spine].set_linewidth(2)

# Límites y cuadrícula
ax.set_xlim(-20, 20)
ax.set_ylim(-20, 20)

# tamaño de los numeros
ax.tick_params(axis='both', which='major', labelsize=10)

# Etiquetas y leyenda
ax.set_xlabel(r"$x$", fontsize=14, loc="right")
ax.set_ylabel(r"$y$", fontsize=14, loc="top", rotation=0)
ax.legend()
ax.set_title("Grafica de la Ecuación", pad=20)
ax.legend(facecolor='none', edgecolor='none')
ax.grid(False)
plt.savefig("ecuacion de las frutas.png", transparent=True, dpi=300)
plt.show()

Este sencillo problema de manzanas y naranjas nos muestra cómo las ecuaciones lineales nos permiten modelar relaciones entre variables de manera clara y predecible. Cada punto en la recta representa una combinación posible que satisface la restricción del problema (gastar 30 €), y la pendiente nos indica cómo cambiaría una variable si ajustamos la otra.

En ciencia de datos y machine learning, este mismo concepto es fundamental: buscamos modelar relaciones entre variables para poder predecir, optimizar o tomar decisiones basadas en datos.

Sistemas Lineales

Un sistema lineal es un conjunto de ecuaciones lineales que resuelves juntas para encontrar valores que satisfagan todas.

Supongamos que a nuestro problema anterior le añadimos una condición. Supón ahora que además de gastar 30 €, queremos comprar exactamente 12 frutas en total. Esa nueva condición se traduce en otra ecuación:

$$x + y = 12$$

Ahora tenemos dos ecuaciones y dos incógnitas $(x, y)$.

$$\begin{cases} 2x + 3y = 30 \\ x + y = 12 \end{cases}$$

Aquí, cada ecuación representa una recta en el plano cartesiano. El punto donde ambas rectas se cruzan es la combinación de frutas que cumple las dos condiciones al mismo tiempo: gastar 30 € y comprar exactamente 12 frutas. Existen varios métodos de resolver los sistemas de ecuaciones.

Método 1: Sustitución:

Despeja una variable en una ecuación.
Sustitúyela en la otra ecuación.
Resuelve.

Cuándo usarlo: Sistemas pequeños (2-3 ecuaciones).

De la segunda ecuación despejamos $x$ y sustituimos en la primera.

$$x + y = 12$$

$$x = 12 – y$$

Sustituimos en la primera ecuación:

$$2(12−y) + 3y = 30$$

$$24− 2y + 3y = 30$$

$$24 − 2y + 3y = 30$$

$$24 + y = 30$$

$$y = 30 – 24 = 6$$

Ahora sustituimos $y$ en la segunda:

$$x + y = 12$$

$$x + 6 = 12$$

$$x = 12 – 6 = 6$$

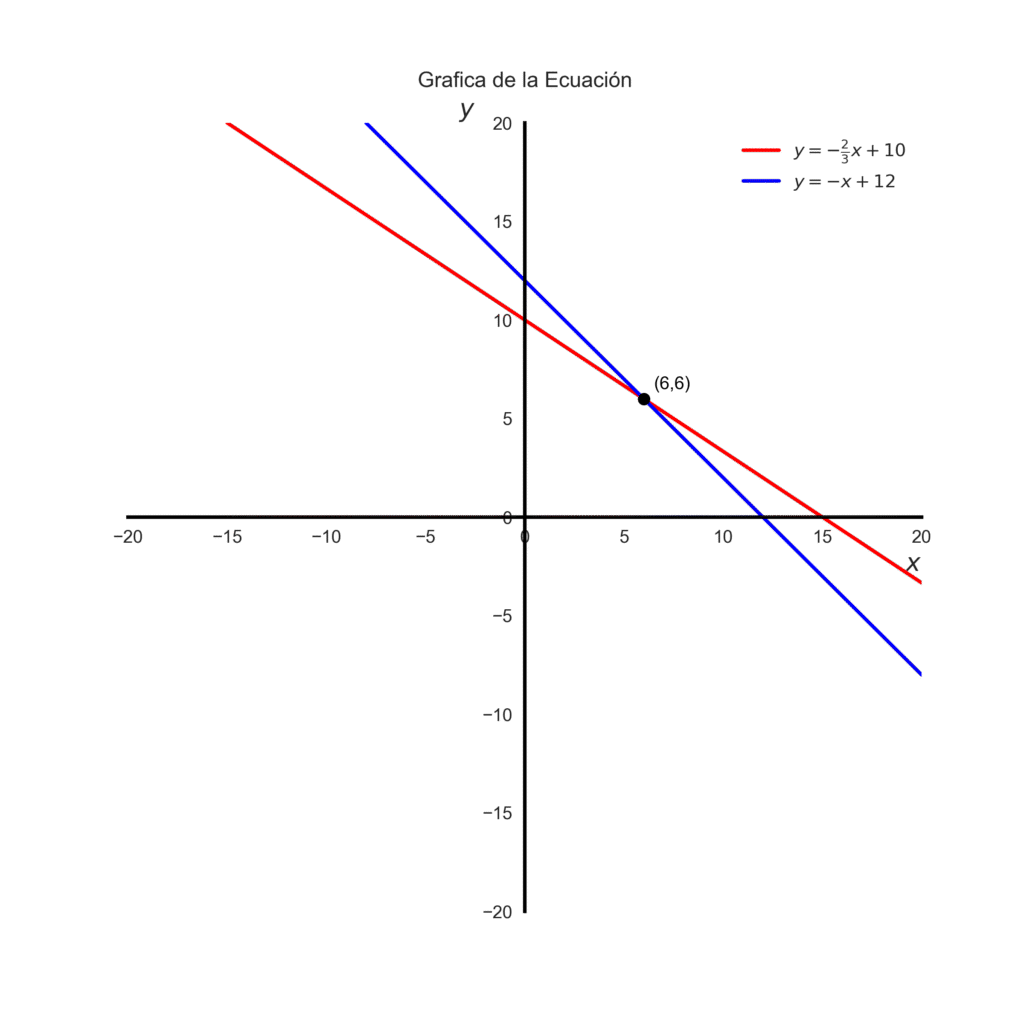
Resultado: $x=6,y=6$, o sea 6 manzanas y 6 naranjas. En el grafico el punto de intersección de las rectas es $(6,6)$.

Con Matplotlib podemos graficar la recta solo con la pendiente y la intersección. En este caso para la segunda ecuacion $m = -1$ y $b = 12$ .

Código del grafico

Código Python de Matplotlib

import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(8,8))
ax.axline((0, 10), slope=-2/3, color="red", linewidth=2, label=r"$y = -\frac{2}{3}x + 10$")
ax.axline((0, 12), slope=-1, color="blue", linewidth=2, label=r"$y = -x + 12$")

# Puntos específicos
ax.plot(6, 6, 'ko', markersize=6)              # dibujar punto
ax.text(x + 0.5, y + 0.5, f"({6},{6})", fontsize=10, color='black')

# Ejes en el centro
ax.spines['left'].set_position('zero')   # eje Y en x=0
ax.spines['bottom'].set_position('zero') # eje X en y=0

# Quitar bordes superior y derecho
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)

# Cambiar color y grosor de los ejes (spines)
for spine in ['left', 'bottom']:
    ax.spines[spine].set_color('black')
    ax.spines[spine].set_linewidth(2)

# Límites y cuadrícula
ax.set_xlim(-20, 20)
ax.set_ylim(-20, 20)

# tamaño de los numeros
ax.tick_params(axis='both', which='major', labelsize=10)

# Etiquetas y leyenda
ax.set_xlabel(r"$x$", fontsize=14, loc="right")
ax.set_ylabel(r"$y$", fontsize=14, loc="top", rotation=0)
ax.legend()
ax.set_title("Grafica de la Ecuación", pad=20)
ax.legend(facecolor='none', edgecolor='none')
ax.grid(False)
plt.savefig("sistemas_de_ecuaciones.png", transparent=True, dpi=300)
plt.show()

import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(8,8))
ax.axline((0, 10), slope=-2/3, color="red", linewidth=2, label=r"$y = -\frac{2}{3}x + 10$")
ax.axline((0, 12), slope=-1, color="blue", linewidth=2, label=r"$y = -x + 12$")

# Puntos específicos
ax.plot(6, 6, 'ko', markersize=6)              # dibujar punto
ax.text(x + 0.5, y + 0.5, f"({6},{6})", fontsize=10, color='black')

# Ejes en el centro
ax.spines['left'].set_position('zero')   # eje Y en x=0
ax.spines['bottom'].set_position('zero') # eje X en y=0

# Quitar bordes superior y derecho
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)

# Cambiar color y grosor de los ejes (spines)
for spine in ['left', 'bottom']:
    ax.spines[spine].set_color('black')
    ax.spines[spine].set_linewidth(2)

# Límites y cuadrícula
ax.set_xlim(-20, 20)
ax.set_ylim(-20, 20)

# tamaño de los numeros
ax.tick_params(axis='both', which='major', labelsize=10)

# Etiquetas y leyenda
ax.set_xlabel(r"$x$", fontsize=14, loc="right")
ax.set_ylabel(r"$y$", fontsize=14, loc="top", rotation=0)
ax.legend()
ax.set_title("Grafica de la Ecuación", pad=20)
ax.legend(facecolor='none', edgecolor='none')
ax.grid(False)
plt.savefig("sistemas_de_ecuaciones.png", transparent=True, dpi=300)
plt.show()

Formato Matricial

La expresión general:

$$y=a_1x_1+a_2x_2+⋯+a_nx_n$$

Es el punto de partida que lleva directamente a la forma matricial de los sistemas lineales. El mismo sistema de ecuaciones de las frutas puede escribirse y resolverse en forma matricial. En la ciencia de datos los datasets son matrices, y resolver sistemas lineales ayuda a encontrar relaciones entre variables.

Partimos del sistema:

$$\begin{cases} 2x + 3y = 30 \\ x + y = 12 \end{cases}$$

En formato matricial:

$$\begin{bmatrix} 2 & 3 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 30 \\ 12 \end{bmatrix}$$

Significado de las partes:

Partes	Significado
$$\begin{bmatrix} 2 & 3 \\ 1 & 1 \end{bmatrix}$$	Matriz de coeficientes: contiene los números que multiplican a las variables (los precios de las frutas).
$$\begin{bmatrix} x \\ y \end{bmatrix}$$	Vector de incógnitas: las variables que queremos encontrar (número de manzanas y naranjas).
$$\begin{bmatrix} 30 \\ 12 \end{bmatrix}$$	Vector de resultados: los valores en el lado derecho (total de dinero y total de frutas).

La forma vectorial compacta del sistema matricial se expresa como:

$$A\vec{x} = \vec{b}$$

Donde:

$A$ –> es la matriz de coeficientes
$\vec{x}$ –> es el vector de incógnitas
$\vec{b}$ –> es el vector de términos independientes

Por tanto:

$$A = \begin {bmatrix} 2 & 3 \\ 1 & 1 \end{bmatrix}, \vec{x} = \begin{bmatrix} x \\ y \end{bmatrix}, \vec{b} = \begin{bmatrix} 30 \\ 12 \end{bmatrix}$$

En ciencia de datos y machine learning esta forma es fundamental porque:

Permite expresar relaciones entre miles de variables en una sola ecuación.
Es la base de la regresión lineal, la reducción de dimensionalidad, y el entrenamiento de modelos.
Toda la manipulación se hace con álgebra matricial, que es más eficiente computacionalmente.

Método 2: Matriz inversa

Determinar si la matriz $A$ tiene inversa (es decir, su determinante es distinto de cero)
Aislar el vector de incógnitas $\vec{x}$.
La forma de hacerlo no es dividiendo, porque no existe la división entre matrices, sino multiplicando por su inversa, denotada $A^{-1}$.

La ecuación de matriz inversa:

$$\vec{x} = A^{-1} \vec{b}$$

Resolviendo el sistema

Para una matriz de dos ecuaciones como la del ejemplo:

$$A = \begin{bmatrix} d & b \\ c & a \end{bmatrix}$$

Determinar su inversa es:

$$A^{-1} = \frac{1}{ad – bc} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}$$

Entonces:

$$A^{-1} = \frac{1}{(2)(1) – (3)(1)} \begin{bmatrix} 1 & -3 \\ -1 & 2 \end{bmatrix}$$

$$A^{-1} = \frac{1}{-1}\begin{bmatrix} 1 & -3 \\ -1 & 2 \end{bmatrix}$$

$$A^{-1} = \begin{bmatrix} -1 & 3 \\ 1 & -2 \end{bmatrix}$$

Este método solo funciona si $A$ tiene inversa, lo que ocurre solo si el determinante de es distinto de cero, como en este caso.

Paso final

$$ \vec{x} = A^{-1}\vec{b}$$

$$\vec{x}=\begin{bmatrix} -1 & 3 \\ 1& -2\end{bmatrix} \begin{bmatrix} 30 \\ 12 \end{bmatrix}$$

$$\vec{x} = \begin{bmatrix} (-1)(30) + (3)(12) \\ (1)(30) + (-2)(12) \end{bmatrix}$$

$$\vec{x} = \begin{bmatrix} -30 + 36 \\ 30 – 24 \end{bmatrix} = \begin{bmatrix} 6 \\ 6 \end{bmatrix}$$

Resultado:

$$x = 6 \\ y = 6$$

Hay algunas operaciones básicas que usaremos constantemente:

Transposición (Aᵗ) → cambia filas por columnas.
Multiplicación de matrices (A·B) → combina vectores o sistemas.
Determinante (det(A)) → indica si el sistema tiene solución única.
Matriz inversa (A⁻¹) → nos permite resolver sistemas como $x=A−1bx = A^{-1} bx=A−1b$.

Estas herramientas son la base de muchos algoritmos modernos de machine learning y análisis de datos.

Forma de la Matriz Aumentada

La matriz aumentada es otra forma de representar un sistema de ecuaciones lineales, pero con un propósito muy concreto: resolverlo más fácilmente mediante operaciones por filas (como en el método de Gauss o Gauss-Jordan). Contiene toda la información numérica del sistema. Trabajar con ella evita reescribir las variables en cada paso.

La matriz aumentada junta la matriz de coeficientes $A$ y el vector de términos independientes $\vec{b}$ en una sola matriz separada por una línea vertical:

$$\begin{bmatrix}\begin{array}{cc|c}2 & 3 & 30 \\ 1 & 1 & 12 \end{array} \end{bmatrix}$$

Esa barra vertical no tiene significado algebraico en sí, simplemente marca la frontera entre los coeficientes del sistema y los resultados.

Método 3: Eliminación Gaussiana

El objetivo de la eliminación es transformar esa matriz con operaciones por filas hasta una forma en la que las variables se lean directamente.
Las operaciones permitidas (elementales por filas) son:

Intercambiar dos filas.
Multiplicar una fila por un escalar distinto de 0.
Sumar a una fila un múltiplo de otra fila.

Estas operaciones no cambian el conjunto de soluciones del sistema: son equivalencias algebraicas.

Paso 1 — Elegir pivote (y, opcionalmente, intercambiar filas)

En esta parte normalmente queremos que el primer elemento de la primera fila (posición (1,1)) sea un buen pivote (idealmente 1 y no 0). En nuestro caso la fila 2 ya tiene un 1 en la columna 1, así que intercambiamos las filas para facilitar cálculos:

Operacion $R_1 \leftrightarrow R_2$ (Row1 y Row2)

$$\begin{bmatrix}\begin{array}{cc|c} 1 & 1 & 12 \\ 2 & 3 & 30 \end{array} \end{bmatrix}$$

Paso 2 — Eliminar la variable $x$ de las filas inferiores

Qué se hace: queremos que en la columna del pivote (columna 1) todos los elementos excepto el pivote sean 0. Si el pivote fuese 0 habría que intercambiar filas para evitar dividir por 0.

Elegimos multiplicar por 2 porque ese número es precisamente lo necesario para que, al restarlo, el coeficiente 2 de la fila 2 quede anulado $(2 − 2 = 0)$.

Operación :$R_2 \leftarrow R_2 – 2R_1$

Multiplicación de la fina 1 por 2:

$$\begin{bmatrix}\begin{array}{cc|c} 2 & 2 & 24 \end{array} \end{bmatrix}$$

Resta la fila multiplicada a la segunda, resultado:

$$\begin{bmatrix}\begin{array}{cc|c} 1 & 1 & 12 \\ 0 & 1 & 6 \end{array} \end{bmatrix}$$

Al hacer esa resta estamos eliminando $x$ de la segunda ecuación.
Esto reduce el sistema a uno triangular superior, que es más fácil de resolver.
La segunda fila ahora es $0x+1y=6$, es decir $y=6$. Hemos aislado una variable.

Paso 3 — Resolver la última ecuación (retro-sustitución) o diagonalizar (Gauss–Jordan)

Ya tenemos el valor de $y=6$, si usamos retro-sustitucion

Retro-sustitución para obtener $x$ sustituyendo y en la primera ecuación:

$$x+y=12x \rightarrow x + 6 = 12 \rightarrow \\ x = \frac{12}{6} \rightarrow x=6$$

Solución por Gaus-Jordan

Eliminamos el $y$ en la primera fila:

$$\begin{bmatrix}\begin{array}{cc|c} 1 & 1 & 12 \\ 0 & 1 & 6 \end{array} \end{bmatrix}$$

Resultado:

$$\begin{bmatrix}\begin{array}{cc|c} 1 & 0 & 6 \\ 0 & 1 & 6 \end{array} \end{bmatrix} \rightarrow x = 6 , y = 6$$

Comprobación

Comprobación en las ecuaciones originales:

$$2x+3y=2(6)+3(6)\\ =12+18=30$$

$$x+y=6+6=12$$

Aplicaciones en Data Science

La generalización del sistema lineal en una matriz aumentada es muy importante porque los modelos lineales en ciencia de datos funcionan exactamente igual:

$$\vec{y} = A\vec{w} + \vec{ε}$$

donde:

$A$ es la matriz de datos (cada fila una observación, cada columna una variable)
$\vec{w}$ son los pesos o coeficientes del modelo (lo que queremos estimar),,
$\vec{y}$ son los valores observados o predichos.
$\vec{ε}$ representa los errores o diferencias entre la predicción y los datos reales.

Esa es exactamente la forma que adoptan los modelos lineales en ciencia de datos y machine learning.

Resolver el sistema equivale a encontrar los valores de $\vec{w}$ que mejor explican o ajustan los datos. Por eso, las ecuaciones lineales y su resolución matricial son la base matemática de muchos algoritmos de Machine Learning.