¿Qué es un Experimento Aleatorio?
Se refiere a cualquier proceso o acción que se realiza bajo condiciones específicas y controladas, pero que, sin embargo, puede producir diferentes resultados en cada realización, sin que sea posible predecir con certeza cuál será el resultado específico en una instancia particular del experimento. La característica distintiva de un experimento aleatorio es esta incertidumbre inherente en el resultado.
Aunque las condiciones sean las mismas, el resultado puede variar en cada repetición.
La característica clave es la incertidumbre del resultado.
Características de un Experimento Aleatorio
- Múltiples resultados posibles:
Puede producir más de un resultado distinto.
Ejemplo: al lanzar un dado, los posibles resultados son ( {1, 2, 3, 4, 5, 6} ). - Resultado impredecible:
No se puede saber con certeza cuál será el resultado antes de realizar el experimento. - Repetibilidad:
El experimento puede repetirse bajo las mismas condiciones, manteniendo las mismas probabilidades para cada posible resultado.
Ejemplos Clásicos
| Experimento | Espacio Muestral |
|---|---|
| Lanzar una moneda | {Cara, Cruz} |
| Lanzar un dado | {1, 2, 3, 4, 5, 6} |
| Extraer una carta de una baraja | 52 posibles resultados |
| Medir el tiempo de vida de un componente | valores continuos en segundos o días |
Resultado (Punto Muestral)
En el contexto de experimentos aleatorios en probabilidad y estadística. Un resultado es definido como el resultado observable de realizar un experimento, el cual, bajo las mismas condiciones, puede variar en cada realización. Esto ilustra la naturaleza aleatoria de tales experimentos, donde no es posible predecir con certeza el resultado específico antes de realizar el experimento.
Ejemplos:
- Lanzar una moneda 4 veces: \(B = {Cara, Cruz, Cara, Cara} \)
- Lanzar un dado 2 veces: \(A = {4, 6} \)
- Extraer una carta: \( C = {«A de corazones»} \)
Espacio Muestral (S o Ω)
El espacio muestral es el conjunto de todos los posibles resultados de un experimento aleatorio. simbolizado comúnmente como S o Ω. Cada resultado individual dentro del espacio muestral es un punto muestral.
$$S = {R_1, R_2, …, R_n}$$
Ejemplos:
- Moneda: \( S = {Cara, Cruz} \)
- Dos monedas: \(S = {(Cara, Cara), (Cara, Cruz), (Cruz, Cara), (Cruz, Cruz)} \)
- Dado de 6 caras: \( S = {1, 2, 3, 4, 5, 6} \)
Algunos espacios muestrales pueden ser infinitos, como lanzar una moneda hasta obtener “Cara”. Aunque sea infinito, sigue siendo contable, ya que podemos enumerar los posibles resultados.
Ejemplo en Python
import itertools
# Lanzar dos monedas
monedas = ["Cara", "Cruz"]
S = list(itertools.product(monedas, repeat=2))
print("Espacio muestral:", S)Salida:
Espacio muestral: [('Cara', 'Cara'), ('Cara', 'Cruz'), ('Cruz', 'Cara'), ('Cruz', 'Cruz')]Eventos
Un evento o suceso se define como uno o cualquier conjunto de resultados posibles de un experimento. El espacio muestral S o Ω de un experimento es el conjunto de todos los posibles resultados individuales, y un evento es cualquier subconjunto de este espacio. Esto incluye desde el conjunto vacío, que representa un evento que nunca ocurre, hasta el espacio muestral completo, que es un evento que siempre ocurre.
- Evento seguro: ocurre siempre → coincide con todo el espacio muestral.
- Evento imposible: nunca ocurre → conjunto vacío \(\emptyset \).
Ejemplo:
Lanzamos dos monedas:
$$S = {(Cara, Cara), (Cara, Cruz), (Cruz, Cara), (Cruz, Cruz)}$$
Evento \(A\): “la primera moneda sea Cara”
$$A = {(Cara, Cara), (Cara, Cruz)}$
Ejemplo en Python
S = [("Cara", "Cara"), ("Cara", "Cruz"), ("Cruz", "Cara"), ("Cruz", "Cruz")]
A = [x for x in S if x[0] == "Cara"]
print("Evento A:", A)Salida:
Evento A: [('Cara', 'Cara'), ('Cara', 'Cruz')]Eventos Mutuamente Excluyentes
Dos eventos son mutuamente excluyentes si no pueden ocurrir al mismo tiempo.
En el lanzamiento de una moneda, los eventos “Cara” y “Cruz” son mutuamente excluyentes.
Ejemplo con Dado:
- ( A ): número impar → {1, 3, 5}
- ( B ): número mayor que 4 → {5, 6}
- Intersección: {5}
⇒ No son mutuamente excluyentes.
Visualización con Diagramas de Venn
Podemos usar matplotlib-venn para visualizar intersecciones de eventos.
from matplotlib import pyplot as plt
from matplotlib_venn import venn2
A = set([1, 3, 5])
B = set([5, 6])
venn2([A, B], set_labels=('A: números impares', 'B: > 4'))
plt.title("Eventos A y B (no mutuamente excluyentes)")
plt.show()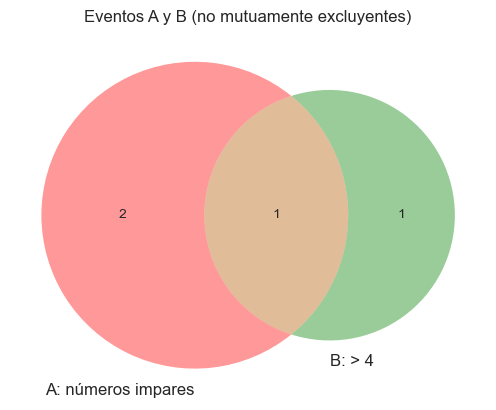
Resumen Conceptual
| Concepto | Descripción | Ejemplo |
|---|---|---|
| Experimento Aleatorio | Proceso con resultado incierto | Lanzar un dado |
| Resultado | Un resultado individual | “5” |
| Espacio Muestral (S) | Conjunto de todos los resultados | {1,2,3,4,5,6} |
| Evento | Subconjunto de S | “número par” = {2,4,6} |
| Eventos Mutuamente Excluyentes | No pueden ocurrir simultáneamente | “Cara” y “Cruz” |
En la práctica estadística
En estadística aplicada y machine learning, estos conceptos son fundamentales porque:
- Permiten modelar la incertidumbre (base de la probabilidad).
- Sirven para definir variables aleatorias y distribuciones.
- Son la base de los métodos inferenciales, como estimación o pruebas de hipótesis.
¿Quieres que el siguiente artículo de la serie sea sobre variables aleatorias (discretas y continuas) o sobre probabilidad condicional y regla de Bayes?