La Distribución de Bernoulli — La base de la probabilidad binaria

En muchas situaciones del mundo real nos enfrentamos a experimentos que solo tienen dos posibles resultados. Por ejemplo:

• Lanzar una moneda: cara o cruz.
• Aprobar o suspender un examen.
• Un cliente hace clic en un anuncio o no lo hace.
• Una lámpara funciona o se funde.

Cuando un experimento tiene solo dos resultados posibles, podemos modelarlo mediante la distribución de Bernoulli, una de las distribuciones más simples y fundamentales en la estadística y la teoría de la probabilidad.

Esta distribución recibe su nombre del matemático suizo Jacob Bernoulli (1655–1705), y es la base de muchas distribuciones más complejas, como la binomial, la geométrica o la beta.

Definición formal

Una variable aleatoria Bernoulli \( X \) puede tomar solo dos valores:

$$X = \begin{cases} 1 & \text{con probabilidad } p \\ 0 & \text{con probabilidad } (1 – p)
\end{cases}$$

Donde \( p \) es el parámetro de la distribución y representa la probabilidad de éxito (por ejemplo, obtener “cara” en una moneda justa).

El parámetro \( p \) cumple que:

$$0 \leq p \leq 1$$

Función de masa de probabilidad (PMF)

La función que describe la probabilidad de cada posible resultado se llama función de masa de probabilidad (PMF):

$$P(X = x) = p^x (1 – p)^{1 – x}, \quad x \in {0, 1}$$

Aunque parezca complicada, en realidad es muy sencilla:

• Si ( x = 1 ): \( P(X=1) = p \)
• Si ( x = 0 ): \( P(X=0) = 1 – p \)

Por ejemplo, si ( p = 0.5 ), tenemos una moneda justa; si ( p = 0.8 ), una moneda sesgada hacia cara.

Esperanza o valor esperado

El valor esperado o esperanza matemática \(E[X] [latex] representa el promedio que obtendríamos si repitiésemos el experimento infinitas veces.

Para una Bernoulli:

$$E[X] = 0 \times (1 – p) + 1 \times p = p$$

Es decir, la esperanza de una Bernoulli es igual al parámetro ( p ).

Si una moneda tiene ( p = 0.7 ) de salir cara, el valor esperado de obtener cara es 0.7.

Varianza

La varianza mide cuánto se dispersan los valores posibles de la variable respecto a su media.
En la Bernoulli, se calcula como:

$$Var(X) = p (1 – p)$$

Esto tiene una interpretación interesante:

• Cuando [latex] p = 0 \) o \( p = 1 \), la varianza es 0, ya que siempre se obtiene el mismo resultado.
• La varianza máxima se da cuando \( p = 0.5 \), es decir, cuando ambos resultados son igualmente probables.

Implementación en Python

Podemos representar la distribución de Bernoulli de varias formas en Python.
A continuación se muestran ejemplos con scipy y también una simulación manual con numpy.

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import bernoulli

# Parámetro de la distribución
p = 0.5

# Posibles valores de X (0 o 1)
x = [0, 1]

# Función de masa de probabilidad (PMF)
pmf = bernoulli.pmf(x, p)

# Graficamos
plt.bar(x, pmf, color='skyblue', edgecolor='black')
plt.xticks([0, 1], ['Fallo (0)', 'Éxito (1)'])
plt.title(f'Distribución de Bernoulli (p = {p})')
plt.ylabel('Probabilidad')
plt.show()

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import bernoulli

# Parámetro de la distribución
p = 0.5

# Posibles valores de X (0 o 1)
x = [0, 1]

# Función de masa de probabilidad (PMF)
pmf = bernoulli.pmf(x, p)

# Graficamos
plt.bar(x, pmf, color='skyblue', edgecolor='black')
plt.xticks([0, 1], ['Fallo (0)', 'Éxito (1)'])
plt.title(f'Distribución de Bernoulli (p = {p})')
plt.ylabel('Probabilidad')
plt.show()

Esto mostrará una gráfica con dos barras, una en 0 con altura 0.5 y otra en 1 con altura 0.5.

Ejemplo: Esperanza y varianza

# Cálculo teórico
mean_theoretical = bernoulli.mean(p)
var_theoretical = bernoulli.var(p)

print(f"Esperanza (E[X]) = {mean_theoretical}")
print(f"Varianza (Var[X]) = {var_theoretical}")

# Cálculo teórico
mean_theoretical = bernoulli.mean(p)
var_theoretical = bernoulli.var(p)

print(f"Esperanza (E[X]) = {mean_theoretical}")
print(f"Varianza (Var[X]) = {var_theoretical}")

Salida:

Esperanza (E[X]) = 0.5
Varianza (Var[X]) = 0.25

Esperanza (E[X]) = 0.5
Varianza (Var[X]) = 0.25

Ejemplo: Simulación con numpy

Vamos a simular 10,000 lanzamientos de una moneda con probabilidad p = 0.7 de salir cara.

# Simulación de 10,000 lanzamientos
n = 10_000
p = 0.7
data = np.random.binomial(1, p, size=n)  # Binomial con n=1 equivale a Bernoulli

# Resultados empíricos
mean_empirical = np.mean(data)
var_empirical = np.var(data)

print(f"Media observada: {mean_empirical:.3f}")
print(f"Varianza observada: {var_empirical:.3f}")

# Simulación de 10,000 lanzamientos
n = 10_000
p = 0.7
data = np.random.binomial(1, p, size=n)  # Binomial con n=1 equivale a Bernoulli

# Resultados empíricos
mean_empirical = np.mean(data)
var_empirical = np.var(data)

print(f"Media observada: {mean_empirical:.3f}")
print(f"Varianza observada: {var_empirical:.3f}")

Salida:

Media observada: 0.703
Varianza observada: 0.209

Media observada: 0.703
Varianza observada: 0.209

7. Interpretación visual

La varianza \( Var(X) = p(1 – p) \) alcanza su máximo cuando \( p = 0.5 \).
Podemos comprobarlo gráficamente:

p_values = np.linspace(0, 1, 100)
variance = p_values * (1 - p_values)

plt.plot(p_values, variance, color='coral')
plt.title("Varianza de la Distribución de Bernoulli")
plt.xlabel("p")
plt.ylabel("Varianza")
plt.grid(True)
plt.show()

p_values = np.linspace(0, 1, 100)
variance = p_values * (1 - p_values)

plt.plot(p_values, variance, color='coral')
plt.title("Varianza de la Distribución de Bernoulli")
plt.xlabel("p")
plt.ylabel("Varianza")
plt.grid(True)
plt.show()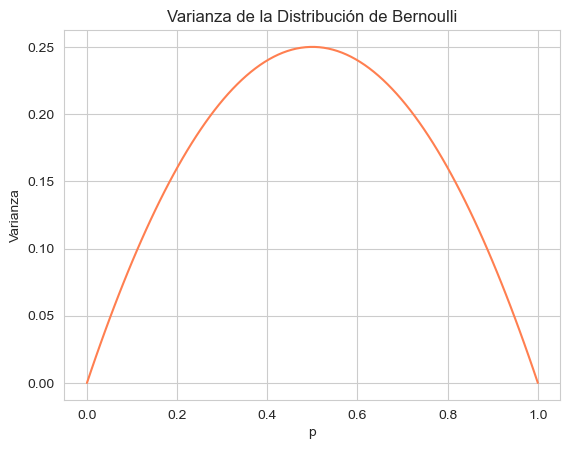

En resumen:

La distribución de Bernoulli es la piedra angular de la probabilidad binaria.
Su simplicidad la convierte en un modelo ideal para entender conceptos más avanzados, como:

• Distribución binomial: suma de varios experimentos Bernoulli independientes.
• Distribución beta: distribución continua conjugada para ( p ) en el contexto bayesiano.
• Procesos de clasificación binaria en machine learning (éxito/fracaso, 1/0).

En resumen: