La probabilidad es una herramienta matemática que nos permite cuantificar la incertidumbre asociada a fenómenos aleatorios. A través de ella, podemos estimar la posibilidad de que ocurran ciertos eventos y construir modelos que representen el comportamiento de sistemas inciertos: desde el lanzamiento de un dado hasta la predicción de enfermedades o el rendimiento de un modelo de Machine Learning.
El estudio de la probabilidad se basa en modelos formales, llamados modelos de probabilidad, que se sustentan en axiomas y reglas fundamentales. En esta sección exploraremos estos conceptos, desde las bases hasta aplicaciones prácticas como la Ley de Bayes o la construcción de un Clasificador de Bayes desde cero.
El Modelo de Probabilidad
Un modelo de probabilidad es un marco conceptual y matemático que permite analizar y predecir el comportamiento de fenómenos aleatorios.
Se apoya en dos componentes esenciales:
- Espacio muestral (Ω): el conjunto de todos los resultados posibles de un experimento aleatorio.
- Regla de probabilidad (P): una función que asigna valores entre 0 y 1 a cada subconjunto del espacio muestral.
El objetivo de este modelo es establecer una ley de probabilidad, una regla que asigne de manera coherente valores no negativos a los eventos, reflejando nuestro grado de confianza o creencia en que ocurran.
Asignación de Probabilidades
La asignación de probabilidades consiste en atribuir valores numéricos a los eventos del espacio muestral. Reflejando la confianza o la creencia en la ocurrencia de esos eventos.
La probabilidad de un evento \( A \), denotada como \(P(A) \), representa qué tan probable es que \( A \) ocurra cuando se realiza el experimento.
Cumple siempre:
$$0 \leq P(A) \leq 1$$
Ley de Laplace
También conocida como la regla de la probabilidad clásica o equiprobable, establece que si un experimento aleatorio tiene resultados igualmente probables, entonces la probabilidad de un evento \(E\) es el número de resultados en \(|E|\) dividido por el número total de resultados posibles en el espacio muestral \(|S|\).
$$P(E) = \frac{|E|}{|S|}$$
Ejemplo práctico:
Un bol contiene 3 bolas rojas y 2 azules.
$$P(\text{Roja}) = \frac{3}{5} = 0.6$$
Si no conocemos los colores, pero sabemos que hay 5 bolas idénticas, la probabilidad de sacar una cualquiera sería ( 1/5 ).
Axiomas de la Probabilidad
Formulados por Kolmogórov (1933), los axiomas definen la base formal de la probabilidad. Son las reglas fundamentales para definir las probabilidades de los eventos dentro del marco de la teoría de probabilidad.
No Negatividad:
El primer axioma establece que la probabilidad de cualquier evento es siempre un número no negativo.
$$ P(A) \geq 0 $$
Normalización:
La probabilidad del espacio muestral completo, representado como \(S\), es igual a 1. Esto significa que es seguro que ocurrirá algún resultado del experimento aleatorio. Se expresa como:
$$P(S)=1$$
Aditividad (Regla de la Suma para eventos disjuntos):
Para dos eventos \(A\) y \(B\) que no pueden ocurrir al mismo tiempo (es decir, son mutuamente excluyentes), la regla de la suma establece que la probabilidad de que ocurra \(A\) o \(B\) es simplemente la suma de sus probabilidades individuales:
$$P(A∪B)=P(A)+P(B)$$
Regla de la Suma para eventos no excluyentes
La regla de la suma es una derivación del axioma de aditivita en caso de que los eventos no sean mutuamente excluyentes. Esta permite calcular la probabilidad de que ocurra al menos uno de dos eventos.
$$P(A \cup B) = P(A) + P(B) – P(A \cap B)$$
Ejemplo (cartas):
Probabilidad de sacar un as o un corazón:
$$P(A \cup B) = \frac{4}{52} + \frac{13}{52} – \frac{1}{52} $$
$$P(A \cup B) = \frac{16}{52} = \frac{4}{13}$$
Ejemplo (dados):
Número impar o mayor que 4:
$$P(A \cup B) = \frac{3}{6} + \frac{2}{6} – \frac{1}{6} $$
$$P(A \cup B)= \frac{4}{6} = \frac{2}{3}$$
Regla de la Multiplicación general
Es un teorema derivado de los axiomas de probabilidad se define a partir del concepto de probabilidad condicional. Permite calcular la probabilidad de que ocurran dos o más eventos a la vez.
Dado que A paso, ¿Cuál es la probabilidad de B?
$$P(A \cap B) = P(A) \times P(B|A)$$
Eventos independientes:
Si A y B son independientes (el resultado de uno no afecta al otro):
$$P(B∣A)=P(B)$$
Entonces:
$$P(A \cap B) = P(A) \times P(B)$$
Ejemplo (cartas sin reemplazo):
$$P(\text{Dos Ases}) = \frac{4}{52} \times \frac{3}{51} $$
$$P(\text{Dos Ases}) = \frac{12}{2652} \approx 0.0045$$
Diagramas de Árbol
Un diagrama de árbol representa de forma visual las posibles secuencias de eventos y sus probabilidades. Cada rama muestra un resultado y la probabilidad asociada.
Ejemplo (dos monedas):
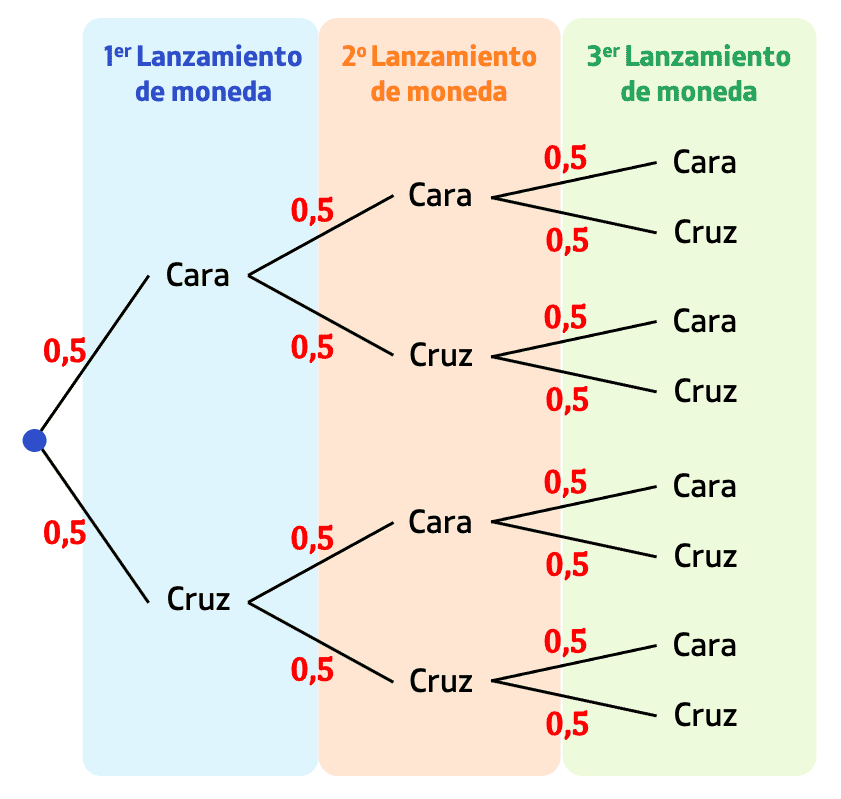
Cada camino representa un evento y su probabilidad se obtiene multiplicando las ramas.
Derivaciones de los Axiomas
A partir de estos axiomas, se pueden deducir varias reglas importantes que son esenciales para el trabajo práctico en probabilidad y estadística.:
Probabilidad del Complemento de un Evento:
Una de las derivaciones más directas es la probabilidad del complemento de un evento. Si A es un evento, entonces el complemento de A, denotado \( A^c\), representa la ocurrencia de \(no−A\). Utilizando los axiomas, se puede demostrar que:
$$P(A^c) = 1 – P(A)$$
Esto se deduce del hecho de que \( A\), y \( A^c\) son mutuamente excluyentes y su unión es el espacio muestral completo, cuya probabilidad es 1.
Probabilidad de Eventos Vacíos y Ciertos:
Directamente de los axiomas, se establece que la probabilidad del conjunto vacío \(∅\), que es un evento imposible, es 0:
$$P(\emptyset) = 0 $$
Asimismo, la probabilidad del espacio muestral completo \( Ω\) , que representa un evento seguro, es 1:
$$P(Ω)=1$$
Monotonicidad:
Si un evento A es un subconjunto de otro evento B, entonces la probabilidad de A es menor o igual a la probabilidad de B. Esto refleja la idea de que la ocurrencia de B incluye la ocurrencia de A junto con posiblemente otros resultados:
$$A \subseteq B \Rightarrow P(A) \leq P(B$$
Probabilidad de unión:
Para dos eventos A y B, la probabilidad de su unión puede ser expresada en términos de las probabilidades de A, B, y su intersección \(A∩B\). Esta regla se aplica incluso si A y B no son disjuntos y se deriva como sigue:
$$ P(A \cup B) = P(A) + P(B) – P(A \cap B)$$
Esto ajusta la aditividad para el caso de eventos que no son mutuamente excluyentes, evitando la sobre contabilización de la intersección de A y B.
Subaditividad:
La subaditividad se refiere a la propiedad de que la probabilidad de la unión de cualquier colección de eventos es menor o igual a la suma de sus probabilidades individuales. Para una secuencia de eventos \(A1,A2,….,An\):
Esta propiedad es particularmente útil para tratar con uniones de eventos que no son necesariamente disjuntos.
Límites de Probabilidad:
Cualquier probabilidad \(P(A)\) para un evento A siempre estará en el rango de 0 a 1, inclusive. Esto se deriva del hecho de que todas las probabilidades son no negativas y que la probabilidad del espacio muestral, el conjunto más grande posible, es 1.
Tablas de Contingencia
Organizan y muestran las probabilidades de combinaciones de dos variables.+
Ejemplo:
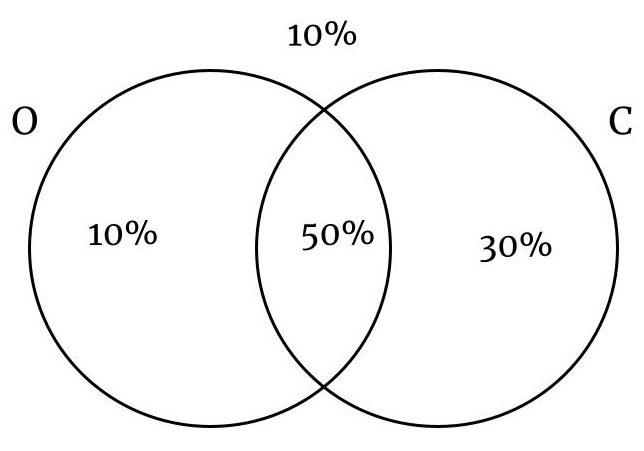
En una ciudad el 60% de las personas tienen ojos negros, el 80% tienen cabello negro y el 50% tienen cabello negro y ojos negros. Si se selecciona una persona al azar, calcule la probabilidad que:
- No tenga los ojos negros.
- Tenga los ojos o cabello negro
- O –> Ojos Negros
- C –> Cabellos Negros
| Variables | Ojos Negros | Ojos No Negros | Total |
|---|---|---|---|
| Cabello Negro | 50% | 30% | 80% |
| Cabello No Negro | 10% | 10% | 20% |
| Total | 60% | 40% | 1.00 |
Las tablas permiten calcular probabilidades marginales, conjuntas y condicionales de manera sencilla.
Modelos de Probabilidad Discretos
Los modelos de probabilidad discretos se ocupan de experimentos donde el número de posibles resultados es finito o contable. Un ejemplo clásico es el lanzamiento de dados, donde los resultados posibles pueden listarse de manera explícita.
Ejemplo: dos dados de cuatro caras.
Supongamos que tenemos dos dados de cuatro caras, donde cada resultado tiene una probabilidad de 1/161/16, podemos construir una tabla que muestre todas las combinaciones posibles de los resultados de los dos dados. Cada dado puede mostrar uno de cuatro resultados posibles (1, 2, 3, o 4), lo que nos da un total de 4×4=164×4=16 combinaciones posibles para los dos dados.
| Probabilidades | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1 | 1/16 | 1/16 | 1/16 | 1/16 |
| 2 | 1/16 | 1/16 | 1/16 | 1/16 |
| 3 | 1/16 | 1/16 | 1/16 | 1/16 |
| 4 | 1/16 | 1/16 | 1/16 | 1/16 |
| Sumas | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 |
| 2 | 3 | 4 | 5 | 6 |
| 3 | 4 | 5 | 6 | 7 |
| 4 | 5 | 6 | 7 | 8 |
Probabilidad de suma par: 8 combinaciones → ( 8/16 = 1/2 )
Probabilidad de al menos un 4: 7 combinaciones → ( 7/16 )
Ejemplo Aplicado: Diagnóstico Médico
Un médico sabe que:
- \( P(\text{Malaria}) = 0.6 \)
- \( P(\text{Tifoidea}) = 0.7 \)
- \( P(\text{Ambas}) = 0.4 \)
La probabilidad de que no tenga ninguna enfermedad:
$$P(\text{No M ni T}) = 1 – P(\text{M} \cup \text{T}) = 1 – [0.6 + 0.7 – 0.4] = 0.1$$
El 10% de los pacientes no tendra ninguna enfermedad.
En resumen
- Las distribuciones de probabilidad son la base para el análisis estadístico, la simulación y la inferencia.
- La probabilidad mide la incertidumbre.
- Todo experimento tiene un conjunto de posibles resultados (espacio muestral).
- Los eventos son subconjuntos de ese espacio.
- Las probabilidades se pueden estimar mediante la frecuencia de los resultados en ensayos repetidos.
- La suma de las probabilidades de todos los resultados posibles siempre es 1.